
今回は機械設計に関連した話題です.機械や構造物を設計する場合,荷重を受ける構造部材が壊れないように頑丈な構造にするわけですが,頑丈かどうかの判断をするための尺度が必要になります.機械が頑丈かどうかの判断には「強度」や「剛性」といわれるものさしが用いられています.
ここでは,機械設計で重要な問題である「はりの曲げ」をとりあげて強度や剛性について考えていきたいと思います.
■5−1 曲げに強い断面形状とは
図5.1 のように片持ばりの先端に力を加えるとはりは曲げられてたわみます.力の大きさとはりの材質は一定とすると,はりのたわみ量を支配しているものはなんでしょうか.直感的にははりの長さと太さといえると思います.たわみ量を小さくするためには,はりを太く短くすればよいわけです.

図5.1 片持ばりの曲げ
しかし本当にはりの長さと断面積が等しければ,たわみ量は同じになるでしょうか?... 次の事実は経験的に知られていると思います.「たわみ量は断面形状に依存する」ということです.ここで次の問題を考えてみてください.
【問題5.1】
図5.1に示す片持ばりの断面形状が図5.2の(a)〜(c)の場合を考えます.この中で最もたわみ量が小さくなる形状はどれでしょうか.
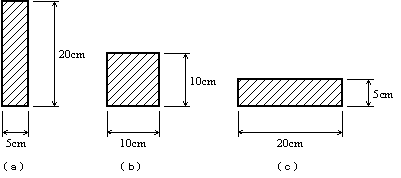
図5.2 はりの断面形状
さてどの形状が曲げにくいでしょうか.答えは(a)ですね.断面二次モーメントという尺度で比較すればよいのです.また断面係数という尺度を用いると曲げ強さを評価することもできます.
■5−2 曲げ応力
物体を曲げようとするときに作用するモーメントのことを曲げモーメントといいます.はりに外力が作用して曲げられている場合,はりの内部にはせん断力と曲げモーメントが作用します.その結果として応力が発生するわけですが,せん断力による応力は曲げモーメントによる応力に比べて無視できる程度ですので,一般に設計では曲げモーメントによる応力だけを問題にします.
図5.3 のようにはりが曲げられている場合,はりの内部がどのような状態になっているかを考えてみます.この場合,はりの上部は縮み下部は伸びるわけですが,この境目には伸びも縮みもしない層があり,これを中立面,また中立面と横断面との交線を中立軸と呼んでいます.さて中立面から距離yにある層はどれだけ伸びるでしょうか.ひずみεは,
………………………………………(5-1)
これより,中立面から距離yにある層で発生している応力(曲げ応力)は次式のようになります.
………………………………(5-2)
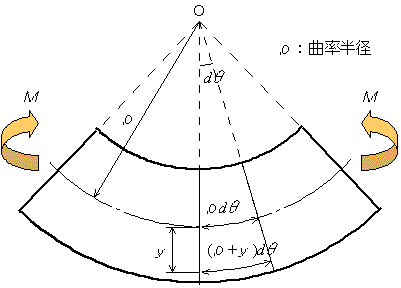
図5.3 曲げ応力
■5−3 断面二次モーメントと断面係数
(1)断面一次モーメント
図5.4 のように中立軸から距離yにある微小要素を考えます.この層では応力σが発生していますから,微小要素に働く軸方向力は,次式で表されます.
…………………………………(5-3)
ここで,はりには外力として軸方向力は働いていません.断面に作用する引張応力と圧縮応力は全体でみると相殺されるので,上式を断面全体にわたって積分すればゼロになります.
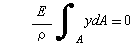
………………………………(5-4)
この式が成り立つ条件は次式となります.
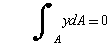
……………………………………(5-5)
これは中立軸まわりの断面積の一次モーメント(断面一次モーメント)の総和がゼロということを表しており,中立軸が断面の図心を通るということを意味しています.

図5.4 微小要素に働く軸方向応力
(2)断面二次モーメント
次に曲げモーメントに関する重要な式を導きましょう.曲げモーメント(符号については絶対値を考える)は力と距離の積ですから,図5.5 のような微小要素では,
となり,断面全体では次式のようになります.

…………(5-6)
ここで,中立軸に関する断面二次モーメントを,
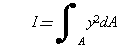
…………………………………(5-7)
とおくと,式(5-6)は次のようになります.
………………………………………(5-8)
ここで,EIを曲げ剛性といいます.
この式より,一定の曲げモーメントMに対し,曲げ剛性EIが大きいほど曲率1/ρが小さく(曲率半径ρが大きく)なることがわかります.すなわち,曲げ剛性EIが大きいほど曲げにくいということです.

図5.5 曲げモーメント
(3)断面係数
式(5-2)と(5-8)より曲率半径ρを消去すると,
………………………………………(5-9)
これより,応力は中立軸からの距離yに比例するということがわかります.すなわち,一番外縁の曲げ応力の値が強さの尺度になるわけです.曲げ応力の最大値と最小値は,図5.6 のように中立軸から下縁までの距離と上縁までの距離をそれぞれ
…………………(5-10)
ここで,
……………………………(5-11)
とおくと,
………………………(5-12)
ここで,
設計では部材に生じる曲げ応力を許容応力以下に抑える必要があります.このためには最大曲げモーメント
……………………………………(5-13)
を計算し,この
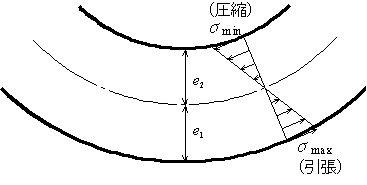
図5.6 最大曲げ応力
ここで断面係数の利用例として,次の問題に取り組んでみてください.
【問題5.2】
図5.7 に示すように中央に集中荷重を受ける両端支持はりの厚さは何mm以上必要でしょうか.ここで許容応力を90MPaとします.
[ヒント]
長さlの両端支持はりが,中央に荷重Wを受けている場合,最大曲げモーメントは中央の位置に発生し,その大きさは次式で表されます.
……………………………………(5-14)
いかがでしょうか,最大曲げモーメントが与えられれば,式(5.13)より35mm以上と答えが求まりますね.
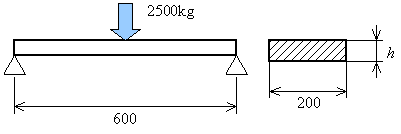
図5.7 両端支持はり(集中荷重)
■5−4 最大曲げモーメントはどこか
問題5.2 のようにはりの設計では最大曲げモーメントの大きさや,それがどこで生じるかが問題にされます.特に最大曲げモーメントが作用する断面で最大曲げ応力が発生しますので,ここが最も破壊しやすい断面ということができます.
最大曲げモーメントの大きさと位置は,はりを仮想的に分割し,力のつりあいとモーメントのつりあいを考えることで求めることができます.例えば図5.8 のように長さがlの両端支持はりに等分布荷重wが作用している場合について考えてみましょう.支点AとBに作用する反力
…………………………………(5-15)
次に仮想的に分割した要素ついて,力のつりあいは,
これよりせん断力は次式のようになります.
………………………………(5-17)
またA点まわりのモーメントのつりあい
……………………………(5-18)
より曲げモーメントは
………………………………(5-19)
と求められます.これより曲げモーメントはx=l/2で最大値

図5.8 両端支持はり(等分布荷重)
このように両端支持はりと片持ばりの場合の最大曲げモーメントは簡単に求めることができますが,両端固定はりの場合は問題が複雑になります.というのも固定はりでは,図5.9 のように支点で固定曲げモーメントが作用するため,未知数が4つに増えてしまうからです.こうなると力のつりあい式とモーメントのつりあい式だけでは未知量を決定することができません.このようなはりを不静定はりといい,はりのたわみ角やたわみなどの幾何学的な条件式を導くことで未知量が決定できます.この他にも不静定はりの解法としては,面積モーメント法やひずみエネルギー法などがありますが,ここでは三連モーメントの定理を適用する方法を紹介します.
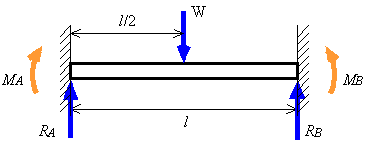
図5.9 両端固定はり(集中荷重)
図5.10のように支点が3個以上あるはりを連続はりといいます.連続はりでは互いに隣り合う三つの支点に働く曲げモーメント
これを連続はりの三連モーメントの定理式といいます.ここで,

図5.10 連続はり
各スパンがそれぞれの中央に集中荷重
……………(5-21)
となります.
では,図5.9に示した中央に集中荷重を受ける両端固定はりの反力と固定モーメントを求めてみましょう.この例では左右対称なので左右の反力と固定モーメントは等しく,
三連モーメントの定理を適用するために,ここで左端に長さ0の仮想スパンを考えて,その端の固定モーメントを0と置きます.すなわち,図5.10の連続はりにて
…………………………………(5-22)
また,力のつりあいより
……………………………………(5-23)
と求まります.
このように未知の反力と固定モーメントを求めることができれば,最大曲げモーメントの大きさと位置は静定はりの場合と同様にして導くことができます.
■5−5 曲げ剛性を改善する方法
昨今では機械装置の高速化やコストダウンを行う目的で軽量化への要求が大きくなっています.ところが,軽量化のために単純に部材の径を細くすると剛性が大幅に低下してしまいます.こうした曲げ剛性の低下を抑えるには部材の断面形状を工夫することが有効です.
例えば,図5.11 に示すように矩形断面のはりをI形になるように肉抜きをします.曲げ剛性はEIで評価できますが,同一材料なので断面二次モーメントIだけで比較します.すると断面二次モーメントについては22%ほど低下してしまいますが,重量的には50%もの軽量化が達成できることがわかります.

図5.11 軽量化と曲げ剛性
さて次の問題は,曲げ剛性を改善する方法の一例です.
【問題5.3】
図5.12の形状ではどちらの剛性が高いでしょうか.

図5.12 中空形状と曲げ剛性
答えは中空形状ですね.同一の断面積の場合には中空形状にすることで曲げ剛性を改善することができます.例えば孟宗竹は曲げに対してとても強いのですが,これは「自然」による改善例といえるのではないでしょうか.
(つづく)
|