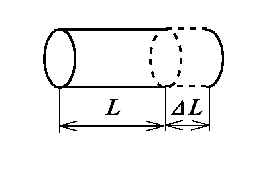
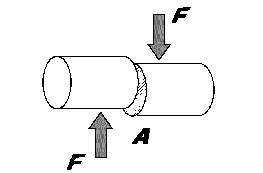
|
�@
�@
�@�����C�A�ڍu������S�b�ƂȂ肢�悢��㔼�ɓ���܂����D����ޗ��͊w�炵���b��𒆐S�ɂ��b��W�J�������Ǝv���܂��D�����ĕ��͂̑��������`���ς��Ă݂܂������������ł��傤���c�c�D
�@���Ă���ł́C�𗧂ޗ��͊w�C�u�n�n�@�C�Ȃ�قǁv�ƍޗ͂̈З͂��������Ē�����悤�ȉ����S�����āC��̓I�Ȃ��b���n�߂邱�Ƃɒv���܂��D
�@
�@
�@
���S�|�P�@�w�ޗ��͊w����x�̎�����
�@
�@�ꌩ�����Ɍ�����w�ޗ��͊w����x�ł����C���͂��܂��܂ȃ_�C�i�~�b�N�Ȏ����������N����܂��D�Ȃ�ǂ�Ȃ��̂�����̂��H�@�ł͂��̎�������߂����Ă݂邱�Ƃɂ��܂��傤�D
�@
�y���4.1�z
�@
�@�}4.1 �̂悤�ȃA���~�j�E���̒i�t�_�Ɉ����d����p����Ƃ��S���̐L�т����߂�D
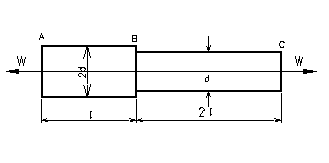
�}4.1�@�i�t�_�̈�����
�@
�@�������ł����H�@�ȒP�����ł��D����ł͂�����͂ǂ��ł��傤�D
�@
�y���4.2�z
�@
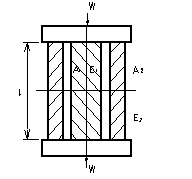
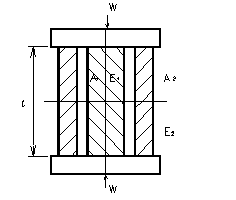 �@�}4.2 �̂悤�ɓ��S�ɔz�u���ꂽ���ꂼ��قȂ�ގ��̉~���Ɖ~�������̔ɋ��܂�Ĉ��k�͂���Ƃ��C�����ɐ����鉞�͂ƈ��k�ʂ����߂�D �@�}4.2 �̂悤�ɓ��S�ɔz�u���ꂽ���ꂼ��قȂ�ގ��̉~���Ɖ~�������̔ɋ��܂�Ĉ��k�͂���Ƃ��C�����ɐ����鉞�͂ƈ��k�ʂ����߂�D
�@
�@
�@
�@
�@
�}4.2�@�َ�̉~���Ɖ~���̈��k�@
�@
�@�O�̖��͍ޗ�������ɂȂ����Ĉ��������Ă�̂ɑ��āC���̖��͕���ɂ�����Ă�ɉ߂��Ȃ��悤�Ȃ��̂ł����C�Ȃ��Ȃ��ǂ����ĈӖ��[���Ȗ��ł��D
�@���ꂩ��C������C���k�Ɋւ��Ă͂���Ȗ�������܂��D�V��ɌŒ肵�ĂԂ牺����ꂽ���_�ɂ́C���Ƃ��_����������Ȃ��Ă��C�_���g�̎��d�ɂ���Ĉ������͂������܂��D���R���[�ɔ�דV��ɋ߂���[�̕��ɑ傫�ȉ��͂������܂��D�����ł���Ȏ������N���Ă��܂��D
�@
�y���4.3�z
�@
�@��[�������[���ׂ����Ċe���f�ʂɐ����鉞�͂��������Ȃ�悤�Ȗ_�̌`������߂�D
�@

�@
�}4.3�@���������̖_
�@
�@���d�ɂ��e�����傫���Ȃ��[�قǑ������Ėʐϓ�����̎��d�C���Ȃ킿���͂���ł����ł����������悤�Ƃ����̂����̖��̎�|�ł��D���������_���g���������̖_�h�ƌĂт܂����C���������ǂ�Ȍ`��̖_�ɂȂ�ł��傤���i�~���`��̖_�ł��傤���H�j�D
�@
�@

�@
�@
 �y���4.4�z �y���4.4�z
�@
�@�R�{�̓�|�_��}4.4 �̂悤�Ƀs���ڍ��i�q���W�x�_�C���߁j���C�c�_�ɉd�v���a�c�̕����ɉ�����Ƃ��C�e�_�ɐ����鉞�͂Ȃ�тɂc�_�̕ψʂ����߂�D
�@
�@
�@
�@
�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}4.4�@�g���X
�@
�@�����������C�������ނ��s���W���C���g�݂̂Őڍ����ꂽ���g�݂��g���X�ƌĂт܂����i��J���ł������Ȃ����߂̂�����̂̓��[�����ƌĂ��j�C������Ɩ��ł��D�������������Ȃ����g���X�͓S���̂悤�ɂȂ�܂����C������ޗ͂̐��E�ł��D���ꂩ��c�c�C
�@
�y���4.5�z
�@
�@�}4.5 �̂悤�ɓ��������̓S���̂`�a�ԂɈ�l�ȑ����̃P�[�u����C���̗��[�b�Ƃc��n�ʂɌŒ肷��D���̎��P�[�u���ɐ�����ő剞�͂����߂�D

�}4.5�@�n�ʂɌŒ肳�ꂽ�P�[�u��
�@
�@�����d����[�v�E�F�C�ȂǂɌ�������i�ł����C���̖��ʼn��͂����������ő����P�[�u�����g���Ă����͂Ȃ�̉����ɂ��Ȃ�܂���D�s�v�c�Ȃ��Ƃł����C������ޗ͂̐��E�ł��D���̂ق��ɂ��c�c�C
�@
�y���4.6�z
�@
 �@�}4.6 �̂悤�ɒ��a��=60mm�̃|���`�Ō�����=5mm�̔ɉ~�E��ł������Ƃ��C�̂���f������400N/mm2�Ƃ��������̑ł��������o��K�v�Ƃ��邩�D �@�}4.6 �̂悤�ɒ��a��=60mm�̃|���`�Ō�����=5mm�̔ɉ~�E��ł������Ƃ��C�̂���f������400N/mm2�Ƃ��������̑ł��������o��K�v�Ƃ��邩�D
�@�܂��|���`�ɐ����鈳�k���͂�1000N/mm2���Ȃ����߂ɂ͔̌����̌��E�͂����炩�D
�}4.6�@�̑ł�����
�@
�@�܂��܂�����܂��\�\�D
�@
�y���4.7�z�c���͗e��
�@
�@�}4.7 �̂悤�ɂR�̕��i����Ȃ鈳�͗e�킪�l20�̃{���g�U�{�Œ��ߕt�����Ă���D������=0.8MPa����p����Ƃ��C�{���g�ɐ�����������͂����߂�D

�}4.7�@���͗e��
�@
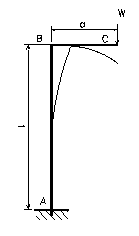 �y���4.8�z�c�k�`�t���[���̂���� �y���4.8�z�c�k�`�t���[���̂����
�@
�@�}4.8 �̂悤�ɂk�`�t���[���̖ʓ��i�t���[���̍�镽�ʓ��j�ɏW���d����p����Ƃ����d�_�̂���݂����߂�D
�@
�@
�@
�@
�@
�@
�@
�@
�}4.8�@�k�`�t���[��
�@
�@
�@�t���[�������̂Ȃ炽��݂܂��C����ނ̂ł���u���̗̂͊w�v�ł͉����܂���D�ό`���l����ޗ͂̐��E�ł�������C���̂���ݗʂ��v�Z�ł���̂ł��D
�@
�y���4.9�z�c�Ȃ�͂�
�@
�@�}4.9 �̂悤�Ȕg���Ȃ߂炩�ȕ��ʂň��k����Ă���D���̂Ƃ��C�����̕ω��ʂ���єg�̃s�b�`�̕ω���
�����߂�D
�@
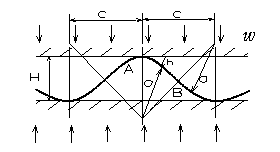
�}4.9�@�g�̈��k
�@
�y���4.10�z�c�،��������̈����i���͏W���j
�@
�@�}4.10�̂悤�ɑ��ʂɔ��aa �̔��~�،������������������̔��z�d���i���͂��v�Ƃ���j�ň����������Ƃ��C�ŏ��f�ʂ`�|�a�ɐ����鉞�͂����߂�D
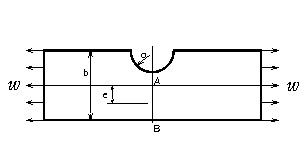
�}4.10�@�،���������
�@
 �y���4.11�z�c���̍��� �y���4.11�z�c���̍���
�@
�@�}4.11�̂悤�ɒ��a���̗��[��]�x�_�̒��̈�[�Ɏ������d�o���č�������Ƃ��̉d�����߂�D
�@
�@
�@
�@
�@
�@
�@
�}4.11�@���̍���
�@
�@
�@�ȏ�݂͂ȁC���̂Â���Ɍg���l�����Ȃ�N�ɂł��g�̉��ŋN���������ł����C�����͂�������ޗ��͊w�̐��E�ŋN���鎖���Ȃ̂ł��D
�@
�@

�@
�@
�@���āC���߂Ă����̖��߂Ă݂�ƁC�����̖�肪���߂Ă���̂́C�T�ˁC
�@�@�@�@���͂����߂�D
�@�@�@�A�ό`�ʁi���k�ʂ₽��݂Ȃǁj�����߂�D
�Ƃ��������ƂɏW���悤�ł��D���͂ɂ��Ă͊�{�I�ɂ͗͂̒ނ荇�����疢�m�ȗ͂����߂��Ƃ����S�ł��D�ό`�ʂ͂��̗͂Ɋ�Â��ăt�b�N�̖@�����狁�܂�܂��D�����Ă����Q�̃v���Z�X���Ɨ����čs���邱�Ƃ�����i���Ƃ��Ă͊ȒP�j�C�݂��Ɋւ�荇���ĘA�����Ă���ꍇ�i����j������܂��D
�@
�@
�@
���S�|�Q�@�����Ђ��݂Ƃ���f�Ђ���
�@
�@��R�b�܂Ői�߂Ă������͂�Ђ��݂ɂ��āC�����ł�����x�܂Ƃ߂Ă����܂��傤�D
�@
�i�P�j���W�n
�@�ƁC���̑O�ɍ��W�n�����߂Ă����܂��D�ʏ퉺�}�̂悤�ɁC�_�̎����ɉ����ĉ����i�����j���C���w�̋��ȏ��Ƃ͈���ĉ����������ɏc���i�����C�d�͂̌�������ɂ��Ă���j���߂�̂���ʓI�ł��D�������C������������Ɏ���Ă���e�L�X�g������܂����C��{�I�ɕς��͂���܂���D�R���s���[�^�v�Z��F����Ԃ�z�肷��ꍇ�ɂ͂��̕����s���������̂�������܂���D
�@

�}4.12�@���W�n
�@
�@�܂��C�L�тƂ���f�ɂ��āC�͂̐������͏�}�̒ʂ�ł��D�������ɂ��Ă͖_�́{���[�ʂɐ��̌����Ɂi�|���[�ʂɕ��̌����Ɂj�����͂��v���X�C���������ĐL�т��v���X�D����f�ɂ��Ă͖_�̐ؒf�ʂ��{�����ނ��c�����̌����Ɂi�|�����ނ��c�����̌����Ɂj�����悤�ȗ͂��v���X�Ƃ��܂��D
�@
�@

�@
�@
�i�Q�j�L�сE�k��
�@�ł͂����ŁC���������̉��͂ƂЂ��݂ł����C�������͎͂��̂悤�Ȃ��̂ł����D
�@
�@�@
�@
�@
�}4.13�@�_�̈�����
�@
�@����C�����Ђ��݂�
�@
�@�@
�@
�@
�}4.14�@�����Ђ���
�@
�@�����ĂЂ��݂Ɖ��͂̊W�́i�t�b�N�̖@���Ƃ����܂����j�C
�@
�@�@
�@
�@�����L�тƗ͂̌`�ŕ\���C�㎮�̗��ӂɖʐς��悶��(4.2)�������Ď����܂��D
�@
�@�@
�@
�@
�i�R�j����f�i����j
�@����f���͎͂��̂悤�Ȃ��̂ł����D
�@
�@�@
�@�@�@�@�@
�@
�}4.15�@�_�̂���f
�@
�@����ł͂���f�Ђ��݂́C

�@
�@�@
�@
�@
�}4.16�@����f�Ђ���
�@
�@�����āC�Ђ��݂Ɖ��͂̊W�́C
�@
�@�@
�@
�@�����L�тƗ͂ŕ\���āC
�@
�@�@
�@
�@
�@
���S�|�R�@�����E���k���猩����L�[�|�C���g�I
�@
�@�ޗ��͊w�̗�����[�߂�ɂ́C�܂����ɓ������Ă݂�̂������ł��D�l���Ă��邾���ł͌����Ă��Ȃ�����������܂����C�����Ⴒ�������Ă��邤���ɍ��܂ł̒m������C�ɂȂ���Ƃ������Ƃ��ԁX����܂��D�Ƃ������C����Ă݂Ȃ��ƕ�����Ȃ����̂ł��c�c�D
�@�ł́C��قǂ߂�����������̒����������グ�邱�Ƃɂ��܂��傤�D
�@
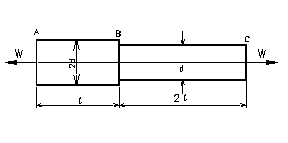
�y���4.1�z
�@
�@�}4.1 �̂悤�ȃA���~�j�E���̒i�t�_�Ɉ����d����p����Ƃ��S���̐L�т����߂�D�������Cl=100mm�C��=15mm�C�v=5.88kN�C�����O���d=73GPa�Ƃ���D
�}4.1�ā@�i�t�_�̈�����
�@
�y��4.1�z
�@
�@�����d�v�́C�_�̌`�͂ǂ��ł���C�����낤���ׂ��낤���C�Ƃɂ����P�{�̖_�ɍ�p���܂��D�܂葾�����ɂ��ׂ����ɂ������������d����p����̂ł��i�������ׂ͍����������Ƃ��āC�ׂ����͑������������Ƃ��ĉd����p����j�D���������āC���̖��͖_�����ƍׂ����ɕ����C�e�X�̐L�їʂ����v���Ă��悢�Ƃ������ƂɂȂ�܂��D��������������Ȋw�I�ɐ������܂��傤�D
�@
�@(1)�����ƂȂ��
�@�i�t�_��i�̕����łQ�ɕ����C���̋��E�ł̔��͂����ꂼ���v�P�C�v�Q ���܂��D
�@
�@
�@���̂Ƃ��C���E�ʂ͓����Ȃ��̂ŁC�݂��̔��͂͒ނ荇���Ă��܂��i�͂̒ލ������^�͊w�I�����j�D����āC
�@
�@�@
�@
�@����C�������ށi�ׂ����ށj�͈ړ����Ȃ��̂ŁC�O���v�Ɣ����v�P�i�v�Q)�͒ނ荇���Ă��܂��i�͂̒ލ������j�D���Ȃ킿�C
�@
�@�@
�@
�@�ȏォ��C
�@
�@�@
�@
�@(2)���������̐L�����k�P
�@�͂ƐL�т̊W�́C��(4.4)�����k�ɂ��ĉ����ĊY���̐��l��������Γ��邱�Ƃ��ł��܂��D
�@
�@�@
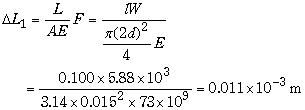 �@�c�c(A) �@�c�c(A)
�@
�@(3)�ׂ������̐L�����k�Q
�@
�@
�@
�@
�@(4)�S���̐L�����k
�@
�@�@
�c(C)
�@
�@������������Ȓ��q�ł��D�ł͎��\�\�D
�@
�y���4.2�z
�@
�@�}4.2 �̂悤�ɓ��S�ɔz�u���ꂽ�C���ꂼ��قȂ�ގ��̉~���Ɖ~�������̔ɋ��܂�Ĉ��k�͂���Ƃ��C�����ɐ����鉞�͂ƈ��k�ʂ����߂�D
�@
�@
�@
�}4.2�ā@�َ�̉~���Ɖ~���̈��k
�y��4.2�z
�@
�@����͑O��Ǝ��Ă���悤�ȋC�����܂����C���͓����悤�ɂ͂����܂���D�ǂ����Ⴄ���Ƃ����ƁC���k�d�v �́C�u�P�{�̖_�c�v�łȂ��u�����Q�{�̖_�i�~���Ɖ~���j�v�ɍ�p���Ă���_�ł��D�܂��̉d���l�ŕ��S���Ă��邽�߂ɁC�ǂ��炪�ǂꂾ���̗͂S���Ă��邩��������Ȃ��Ƃ������ƂȂ̂ł��D�����炭�͈��k�ɋ����������ꂾ���傫�ȗ͂������Ă���ɈႢ�Ȃ��Ɛ����ł��܂����C���F�����ł�������܂���D�����œ��������߂�킯�ɂ͂����܂���D
�@���̂悤�Ȃ��ƂŁC�����ƂȂ�͂��m��ł��Ȃ��킯�ł�����C���������ĉ��͂͂�����ʂł��鈳�k�ʂ�������Ȃ��Ƃ������ƂɂȂ�̂ł��D
 �@���̈Ӗ��ł�����ƕς������Ȃ̂ł��D �@���̈Ӗ��ł�����ƕς������Ȃ̂ł��D
�@
�@�����łǂ����邩�D����͕͗͂����������̂Ƃ��ĂƂ肠�����`���I�ɓ����i���ʂł���ψʁj�����߂Ă݂܂��D�����ŕψʂɊւ�����������߁C�����͂̊m���ƂɃt�B�[�h�o�b�N���Ă��C�Ƃ������Ƃ��l���܂��D
�@
�@(1)�����ƂȂ��
�@�~������щ~���ɓ����͂����ꂼ���v�P�C�v�Q�Ƃ��܂��D�����̊m�肵���l�͕�����܂��C���Ȃ��Ƃ����̂��Ƃ����͕������Ă��܂��i�͂̒ލ������j�D
�@
�@�@
�@
�@(2)���ʂłȂ鈳�k��
�@�~������щ~���̈��k�ʂ����ꂼ����1�C��2�Ƃ��܂��D���̈��k�ʂ́C�O�̗��Ɠ��l�Ɏ��i4.4�j�Ɋ�Â��Ď��̂悤�ɋ��߂��܂��D
�@
�@�@
�@
�@(3�j�ψʂɊւ������
�@�Ƃ肠���������͋��߂��܂������C���R�v�P�C�v�Q�����m��ł��̂Ŗ{���ɋ��܂����킯�ł͂���܂���D�������C���̒i�K�Ńn�b�L�����Ă���d�v�ȏ���������o����܂��D����͉~�����~�������̔ŕ��s�ɋ��܂�Ă���̂łǂ�����������k�ʂ��Ƃ������Ƃł��i�ό`�̒ލ������^�w�I�����j�D���Ȃ킿�C
�@
�@�@
�@
�@���̕ό`�Ɋւ���������قǂ̗͂����߂�X�e�b�v�ɖ߂��Ă���āC���߂ĉd�̌v�Z����蒼���Ă݂܂��D
�@
�@(4)���E�����ƂȂ��
 �@��(D)�����ł͌��߂��Ȃ������d�v�P,�v�Q�́C�w�I������(F)���t�B�[�h�o�b�N���Ă�邱�ƂŁi�v�P�C�v�Q�Ɋւ���A���������������āj�m�肵�Ă�邱�Ƃ��ł���̂ł��D���Ȃ킿�C �@��(D)�����ł͌��߂��Ȃ������d�v�P,�v�Q�́C�w�I������(F)���t�B�[�h�o�b�N���Ă�邱�ƂŁi�v�P�C�v�Q�Ɋւ���A���������������āj�m�肵�Ă�邱�Ƃ��ł���̂ł��D���Ȃ킿�C
�@
�@�@
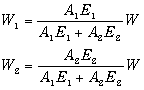 �@�@�c�c�c�c�c�c�c�c�c�c�c(G) �@�@�c�c�c�c�c�c�c�c�c�c�c(G)
�@
�@���ꂩ�番����悤�ɁC�d�v���`�P�d�P�C�`�Q�d�Q�̔䗦�ɂ���ĉ~���Ɖ~���ɕ��z����Ă��邱�Ƃ�������܂��D�`�d�͐L�э����ƌĂ�܂�����i��R�b�ɓo��j�C�m���Ɂu���k�ɋ����������ꂾ���傫�ȗ͂������Ă���ɈႢ�Ȃ��v�Ƃ��������������ŗ��t�����܂����D
�@
�@(5)���͂ƈ��k��
�@���Ĉȏ�ŁC�e�X�̕��ނɍ�p����͂����܂����̂ŁC�S�|�Q�߂̌����ɑ����ĉ~������щ~���ɐ����鉞�͂Ȃ�тɈ��k�ʂ����̒ʂ苁�܂�܂��D
�@
�@�@
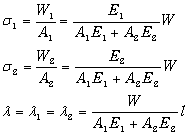 �@�@�c�c�c�c�c�c�c�c(H) �@�@�c�c�c�c�c�c�c�c(H)
�@
�@

�@
�@
���S�|�S�@����f�̊�{���
�@
�@�c�O�Ȃ���C��������������܂���D���������̘b�肪�����Ȃ��Ă��܂��܂����D�����ł͂���f�̖�����C�U�b�Ɖ��������ɒv���܂��D
�@
�y���4.3�z
�@
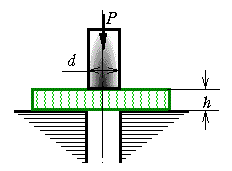 �@�}4.6 �̂悤�ɒ��a��=60mm�̃|���`�Ō�����=5.0mm�̔ɉ~�E��ł������Ƃ��C�̂���f������400N/mm2�Ƃ��������̑ł��������o��K�v�Ƃ��邩�D �@�}4.6 �̂悤�ɒ��a��=60mm�̃|���`�Ō�����=5.0mm�̔ɉ~�E��ł������Ƃ��C�̂���f������400N/mm2�Ƃ��������̑ł��������o��K�v�Ƃ��邩�D
�@�܂��|���`�ɐ����鈳�k���͂�1000N/mm2���Ȃ����߂ɂ͔̌����̌��E�͂����炩�D
�}4.6�ā@�̑ł�����
�@
�y��4.3�z
�@
�@���̖��͊�{�I�ɂ͉��͂Ɍ��y���Ȃ���C�͂̒ނ荇���������l���ĉ���������ł��D�Ƃ���ŁC�ޗ��͊w�ɂ����ė͂̂�͂̃��[�����g�ނ荇�����l����Ƃ��ɂ́C���̂��ό`����O�̏�Ԃł��̒ނ荇�����l���ď��������܂��D���̈Ӗ��ł́u���̗̂͊w�v�Ɠ��l�̎葱���Ƃ�����ł��傤�D
�@
�@���āC���̖��ɂ�����͂̒ނ荇���́C�ł��������o�Ƒł�������錊�ɐ����邹��f�������̍��͂��������Ƃ����̑ς�������E�Ƃ������ƂɂȂ�܂��D���������āC
�@
�@
�@
���̂���f�ʂ̖ʐ��`�́C
�@
�@
�@
����āC�ł������͎͂�(J)����(I)�ɑ�����C
�@
�@
�@
�@�ł������͂́C��(K)�ɔ̂���f�������̊Y�����l�������āC
�@
�@�@
�@
�@����C�̌����̌��E�́C�|���`�̈��k���́C���Ȃ킿�C�ł������͂��|���`�̉��f�ʐςŏ������l��1000N/mm2���Ă͂Ȃ�Ȃ��Ƃ����v������C
�@
 �@�c�c�c�c�c�c(L) �@�c�c�c�c�c�c(L)
�@
�@�|���`�Ɣ��̊Ԃɂ͏�L�̂悤�ȊW�����邱�Ƃ��킩��܂��D�����āC�|���`�̒��a��60mm�̂Ƃ��̑ł���������̌��E�́C
�@
�@�@
�@
�i���j
�@
�@
�@
���@�@���@�@��
�@
�\���ҁ@�͂�̘b
�@
�@
|