|
�M�͊w����
�\��Q�b�@�M�͊w�̈ʒu�t��
�@ �`�@�M�Ǝd���@�`
�@
�@���b�ł́q�M�͊w�r�Ƃ͉�������o�����C�q���x�r�Ɓq�M�r�ɂ��čl���Ă��܂����D���b�ł́q�M�͊w�r�ɂ�����q�d���r�ɂ��čl���Ă������Ƃɂ��傤�D
�@
���Q�|�P�@�M�͊w�Ƃ��Ắq�d���r�Ƃ�
�@�M�͊w�ł́q���́r�ɂ���ĂȂ����d���������Έ����܂��D���̐߂ł͎d���ɂ��čl����O�ɁC�q���́r�ɂ��ė�����[�߂���ŁC�q���́r�����E�ʂ���ĊO���ɂȂ��q�d���r�ɂ��čl���čs�����Ƃɂ��悤�D
�i�P�j���@��
�@�}2.1�̓S�����D���������ꂽ��C�ɂ���Ăӂ����ł���Ƃ��̗͊W���������}�ł��D���D���̋�C�ɂ͕��D�̊O������̑�C�̗͂ƕ��D�̃S�����k�����Ƃ���͂��|�����Ă��܂��D���D���̋�C�͂��̓�̗͂𑫂����͂Ɠ����傫���Ŕ�
|
|
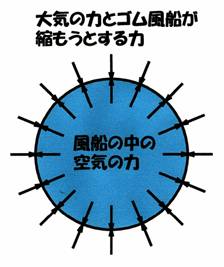
�}2.1�@���D�̗͊W
|
|
�Ό����̗͂������Ă��܂��D���̂Ƃ����D�̕\�ʐς�A [m2]�C ���D���̋�C�̎��͂�F [N]�Ƃ����ꍇ�C�P�ʖʐς�����̗͂ŕ\������������ʓI�ȗʂƂ��Ĉ����܂��D���ꂪ�q���́r�ŁC
�L����P�C�P�ʂ�[N/m2] ���邢��[Pa]���Ȃ킿�p�X�J���ŕ\����܂��D
���������āC�q���́r�͎����ŕ\����܂��D
F
P �� �\�@�@ [Pa]�@�@�@(2.1)
A
�܂��C���D�̃��f���ŕ�����悤���q���́r�͕��D�����̑S�Ă̕ǂɑ��ē���
�悤�ɓ����܂��D
�@ �@
�i�Q�j�d�@��
��ʂɁC��������͂Ɠ��������ɕ��̂��^������Ƃ��C�q�d���rW �͗͂̑傫����F�C���̂̈ړ������� s �Ƃ���ƁC�ȉ��̂悤�ȊW������܂��D
W��F s�@�@�@�@�@[J]
(2.2)
�����ɁC�d���̒P�ʂ�[J]�C�W���[����p���C1J��1Nm�ł��D
���ɐ}2.2�̂悤���M�͊w�I�d�����f���C���Ȃ킿�C�s�X�g���ƃV�����_���ɋC�̂������Ă���n�ɂ����āC�f�ʐ�A[m2]�����s�X�g����s [m] �ړ������ꍇ�ɂ��čl���Ă݂܂��傤�D���̏ꍇ�s�X�g�����C�̂���Ă����F�͎�(2.1) ���C�q���́rP�ƃs�X�g���̖ʐ�A�̐ςŗ^�����܂��D���Ȃ킿�C
F��PA�@�@�@�@�@[N] �@�@�@�@�@�@�@�@�@�@�@�@ (2.3)
���̎�(2.3)����(2.2)�������ƃs�X�g�����q�d���rW �͎����̂悤�ɂȂ�܂��D
W��PA s��PV�@�@[J] �@
�@�@�@�@�@�@�@�@�@�@�@�@ (2.4)
�����ɁCV�̓s�X�g�����ړ��������Ƃɂ��̐ϕω���A s�ł��D
�ȏ�Œ�`���ꂽ�C�q���́rP�C�q��Ή��x�rT������q�̐��rV�̂R�̕����ʂ����܂�Ƃ��̂Ƃ��̋C�̂��q��ԁr�����܂�܂��D�����R�̕����ʂ��q��ԗ��r�ƌĂ�Ă��܂��D
|
|
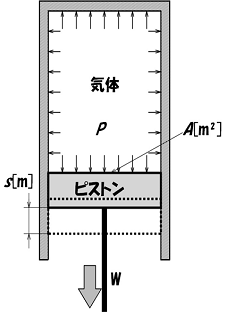
�}2.2�@�M�͊w�I�d�����f��
|
|
���Q�|�Q�@�n���O���ɂȂ��d���q��Ύd���r�̓���
�@
�@�}2.3�Ɏ������悤�ɁC�����̋C�̂��s�X�g���ƃV�����_�ō\��������Ԃɕ����߂��Ă���ꍇ(�q�����n�r)�ɂ��čl���Ă݂܂��傤�D���̋C�̂��q��ԁr
1�i����P1�C�̐�V1�C��Ή��xT1�j�����q��ԁr2 �i����P2�C�̐�V2 �C��Ή�
�xT2�j�ɖc�������Ƃ��C �s�X�g�����ړ����邱�Ƃɂ���ĊO���ւȂ��d���������Ƃ߂Ă݂܂��傤�D
|
|
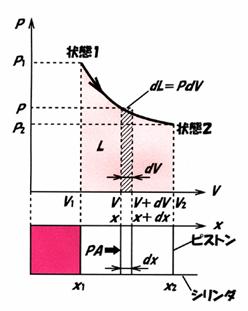
�}2.3�@��Ύd���i�����n�j
|
|
���̃s�X�g�����ʒux����x�{dx�܂Ŕ����������ړ������Ƃ��܂��D���̊Ԃ̈ړ������͔����Ȃ̂ň��͕ω��͂Ȃ��ƍl�����܂�����C���̂Ƃ��C�̂��s�X�g������ĊO���ɂȂ��q�d���r�́C�s�X�g���̒f�ʐς�A[m2]�Ƃ���ƁC�����ŗ^�����܂��D
PAdx [J]
�����ŁCAdx�͔����̐ϕω�dV�Ə����������܂��D
���������āC���̂Ƃ��O���ɑ��ĂȂ��������d���� dL�Ƃ���ƁC�����̂悤��
�Ȃ�܂��D
dL��PdV�@�@[J]
(2.5)
���������āC�����߂�ꂽ�C�̂����1������2�ɏ�ԕω������Ƃ��ɁC�O���ɑ��ĂȂ����q�d���r�͎����ŗ^�����܂��D
���2
2
L ����@dL ���� PdV �� �ʐ�12V2V11�@�@[J]
(2.6)
���1
1
���̎��ŗ^������q�d���r���q��Ύd���r�ł��D
�@�����߂�ꂽ�C�̂̎��ʂ�m[kg]�Ƃ���ƁC�P�ʎ��ʂ�������q��Ύd���r��l��L/m�ŕ\����܂��D��(2.5)�̔����`���ɑ��ẮC�ȉ��̂悤�ɏ����������܂��D
dl��Pdv�@�@�@[J]
(2.7)
�����ɁCv�͎����ŗ^�������̐ςŁC���x��[kg/m3]�̋t���ł��D
v��V/m�@�@�@[m3/kg]
(2.8)
��(2.7)��ϕ�����ƁC�����̂悤�ɂȂ�܂��D
2
2
l ���� dl ���� Pdv�@�@�@�@[J/kg]
�@�@�@�@�@�@
(2.9)
1
1
���Q�|3�@�n�ɊO�����炳���d���q�H�Ǝd���r�̓���
�@
�@���ɁC�}2.4�Ɏ������悤�ɁC�V�����_�̒[�ɋz����A�Ɣr�C��B�������Ă���C�C�̗̂����C���o������ꍇ(�q�J�����n�r)�ɂ��čl���Ă݂܂��傤�D���߃s�X�g���̓V�����_�̍��[�ɂ���C�z����A�Ɣr�C��B�͕��Ă���Ƃ��܂��D���܁C
�@�z����A�݂̂��J���C����P1�̋C�̂�������1�܂ł��Ȃ킿�̐ς�V1�ɂ�
��܂Ńs�X�g���������܂��D���ɁC�A�z����A�������C�C�̂����2���Ȃ킿����P2�ő̐�V2�܂Ńs�X�g����������܂��D�����āC�B�r�C��B���J����C����P2���C�̂��S�ăV�����_�̊O�ɏo�čs�����Ƃɂ���āC�s�X�g�������߂̏�Ԃɖ߂���܂��D�����R�̉ߒ��ɂ����āC�C�̂��s�X�g������āC�O���ɑ��ĂȂ��q�d���r���l���Ă݂܂��傤�D
�@ �̉ߒ��ɂ����ẮC����P1�̋C���͒f����A�̃s�X�g�����ʒux1�܂ʼn����܂��̂ŁC�s�X�g�����C�̂�����q�d���r�͎��̂悤�ɂȂ�܂��D
P1Ax1��P1V1
�A �̉ߒ��ɂ����ẮC�����߂�ꂽ�C�͈̂ȉ��̂悤�ȁq��Ύd���r�����܂��D
2
�� PdV
1
�B �̉ߒ��ɂ����ẮC����P2�̋C���̓s�X�g����x2 ���珉�߂̈ʒu�܂Ŗ߂��܂��̂ŁC �s�X�g�����C�̂ɂȂ����q�d���r
�� �ȉ��̂悤�ɂȂ�܂��D
P2Ax2��P2V2
|
|
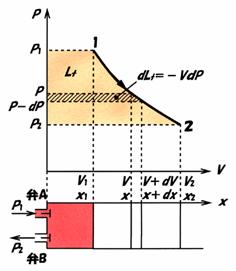
�}2.4�@�H�Ǝd���i�J�����n�j
|
|
���������āC��������ї��o����C�̂��O���ɂȂ��q�d���rLt�͎����̂悤�ɂȂ�܂��D
2
�@�@2
Lt ��P1V1�{�� PdV �|P2V2 ���|�� VdP
[J] (2.10)
1
1
���ʐ�12P2P11
���̎��ŗ^�������q�d���r���q�H�Ǝd���r�ł��D�����\���͈ȉ��̂悤�ɂȂ�܂��D
dLt ��VdP�@�@[J]
(2.11)
�P�ʎ��ʂ�����ł͎��̂悤�ɕ\���܂��D
dlt ��vdP�@�@[J]
�@(2.12)
�@�\���ҁ@�̑�Ȃ�@���P�`�M�͊w�̑��@��
�@���b�ł͔M�͊w�ɂ�����d���ɂ��čl���Ă��܂����D����́q�M�r�Ɓq�d���r�̊W�C�q�G�l���M�[�ۑ����r�C�q�����G�l���M�[�r����сq�G���^���s�[�r�Ƃ������M�͊w�I�Ȑ��p��̒�`��������ŁC�q�M�͊w�r�ɂ�����d�v�Ȗ@���̈�ł���q�M�͊w�̑��@���r�ɂ��čl���čs�����Ƃɂ��悤�D
�@
�@�i���j
|