
■5−6 板ばねのばね定数の求め方
(1)たわみ量
これまで,はりの曲げ強さについて説明してきました.機械の設計では,はりが変形して他の部材と干渉しないかどうかの検討も行う必要があります.検討した結果,たわみ量が許容できない場合には曲げ剛性を高めるわけです.
はりの最大たわみδは次式で求めることができます.
…………………………………(5-24)
ここで,係数αははりの種類と荷重の状態によって決まります.例えば図5.13に示すような先端に集中荷重を受ける片持ばりではα=3であり,最大たわみδは,
…………………………………(5-25)
となります.この式は荷重Pに対するたわみ量δの関係を表したものなので,図5.13は片持ちの板ばねと考えることもできます.この場合,ばね定数kは板の幅b,板厚hとして,
……………………………………(5-26)
なので,
……………………(5-27)
となります.
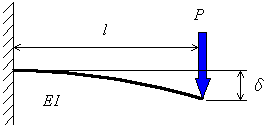
図5.13 片持ばりのたわみ量
片持ばり以外の例では,中央に集中荷重を受ける両端支持はりではα=48であり,両端固定はりではα=192となります.
では次の問題に取り組んでみましょう.
【問題5.4】
図5.14に示す長さl=300mmの軸の中央にP=300Nの集中荷重がかかっています.許容できるたわみ量δを0.01mmとして,両端支持および両端固定の場合について軸径を求めてください.ここで,ヤング率をE=206GPaとします.
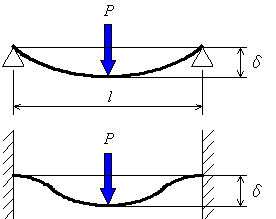
図5.14 はりのたわみ
答えは,両端支持では36mm,両端固定では26mmとなります.このように両端固定とすることで,変形しにくくなり,細い軸ですむので材料費も節約できることがわかります.もう一問,取り組んでみましょう.
【問題5.5】
問題5.4の両端支持はりの場合について考えます.たわみ量δを0.005mmに抑えるように仕様変更してください.要求を効率的に満足するには,どの仕様を変更すればよいでしょうか.
さて,この場合のたわみ量は,
………………………………(5-28)
となりますので軸径d,または長さlを変更すればよいです.軸径については4乗で,長さについては3乗で効いてきますので,dの場合は36mmを43mmに,lの場合は300mmを238mmに変更すればよいわけです.
(2)危険速度
はりの変形は,機械の位置精度の低下や部材間の干渉などの要因となりますが,振動にも関係してきます.例として,回転体を有する機械を考えてみましょう.
図5.15に示すように,角速度ωで回転している回転体に偏心εがある場合,遠心力Poが生じます.
この遠心力により軸がδだけたわむので,動的つりあい状態における遠心力Pは,
これが軸の復原力kδとつりあいますので,
ここで,ばね定数kは,はりの最大たわみの関係から,
……………………………………(5-32)
式(5-31)と式(5-32)より,たわみδは次式となります.
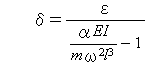
……………………………(5-33)
この式の右辺の分母が零,すなわち,
……………………………(5-34)
のときにたわみδは無限大となります.このときの回転速度を
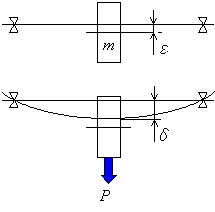
図5.15 偏心している回転体
ここで式(5-34)でαの値をどうするかということが問題ですが,軸を両端支持はりと考えるとα=48となりますし,両端固定はりと考えた場合にはα=192となります.このように両端固定はりにすると剛性を4倍も高くすることができるわけです.
しかし,実際にはどちらと考えて設計すればよいでしょうか.例えば軸の支持に深溝玉軸受を用いている場合には,転がり軸受ではすきまがありますので,図5.16のように,軸受が1つでは両端支持はり,軸受けを2つ並べた場合には両端固定はりとしてモデル化すればよいわけです.
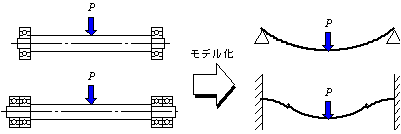
図5.16 回転軸のモデル化
■5−7 ばねがばねで無くなるとき
はりのたわみの式(5-24)を用いれば,設計時に変形量について検討できるわけですが,注意すべき点があります.それは式(5-24)は弾性限度内でのみ成り立つということです.ここで弾性限度を超えるとどうなるのでしょうか.金属材料では弾性限度を超えると塑性変形を生じて急激に変形が大きくなります.しかし荷重については弾性限度を超えても極限荷重までは耐えることができます.このように弾性限度を超えた曲げのことを塑性曲げといい,断面全体が降伏するときの曲げモーメントを全塑性曲げモーメントといいます.
例えば図5.17に示すような,中央に集中荷重を受ける両端支持はりの場合,中央での曲げモーメントが全塑性曲げモーメントに等しくなると,中央断面は全てが塑性部分となり(塑性関節ができたといいます),はりは全体が不安定となって崩壊します.このときの荷重を崩壊荷重といいます.このように弾性限度を超えたはりは,もはや板ばねとよぶことはできません.
もちろん通常の機械設計では最大使用応力として比例限度以下の設計値を用います.このような設計法に対し,構造物の設計法では材料を有効に利用し軽量化を図るための手法として,全塑性曲げモーメントを基準に考える塑性設計法というものがあります.
塑性設計法は建築構造物の設計分野で主に発展してきた考え方で,大地震など発生確率が低い強大な外力に対して弾性範囲内で設計するのは不経済であることから,部材や接合部の一部塑性化を許すというものです.
両端支持はりのような静定はりでは、上述のように塑性関節を生ずるとすぐに崩壊しますが,両端固定はりのような不静定はりでは,一箇所に塑性関節が生じたとしてもすぐには崩壊せず,十分な数の塑性関節が形成されて全体が不安定となるまでは崩壊に至りません.
このように塑性設計法では,限界状態として崩壊荷重を選ぶことができ,合理的な手法と考えられています.
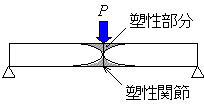
図5.17 塑性曲げ
■5−8 強度不足ではないはずですが
はりの曲げ強さを考慮して設計したつもりでも,機械が破壊してしまう場合があります.「こんなはずでは…」とならないために注意すべき点を挙げておきます.
(1)座屈
これまでの話の中では,軸方向の力は考えていませんでした.ここでは軸方向の圧縮力を受ける棒をとりあげます.これは「はり」ではなく「柱」と呼ばれています.
まず柱の強さを考えてみましょう.柱に圧縮力をかけていきますと柱は降伏し,最後は破壊にいたるわけです.部材として柱を使用する場合には,この降伏点より小さな許容応力を用いて設計します.
例として,一辺が105mmの正方形断面の柱,いわゆる三寸五分柱を考えます.許容圧縮応力を6MPa(61kgf/cm2)とすると,最大使用荷重は66kNとなり,6.7t程度までの荷重を支えることができるはずです.
しかし,この考え方は必ずしも正しくはありません.なぜなら圧縮力が許容応力以下でも,図5-18に示すように柱が突然側方に曲がって逃げる現象が発生する場合があるからです.この現象を座屈といいます.このときの座屈荷重は,次式に示すオイラーの公式で求めることができます.
…………………………………(5-35)
ここで,nは柱の両端の支持方法により定まる係数で,
(a)一端固定,他端自由端 n=0.25
(b)両端とも回転端 n=1
(c)一端固定,他端回転端 n=2.046
(d)両端とも固定端 n=4
となります.通常は荷重を支持する構造として自由端を有する(a)の場合は考えられません.このため(b)〜(d)の値をとると考えられます.設計時には安全を考えてn=1とするとよいでしょう.
式(5-35)から,座屈荷重は柱の曲げ剛性EIと長さlにのみ依存することがわかります.そして,断面積をA,断面二次半径をkとすると
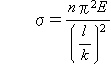
…………………………………(5-36)
となります.ここでl/kを細長比といい,柱の細長さの尺度です.またここで注意すべき点は,オイラーの公式は棒の比例限度内での曲げの式をもとにしています.ですから細長比が小さくなり座屈応力が比例限度を超えた場合には適用できません.この場合には,ランキン,テトマイヤー,ジョンソンなどの実験公式で計算することになります.
ここで,先ほどの三寸五分柱の例を式(5-35)で計算してみましょう.柱の長さl=4m,ヤング率E=6GPa(61tonf/cm2)としますと,座屈荷重は37kNとなり,66kNで使用した場合には柱は座屈してしまうことがわかります.
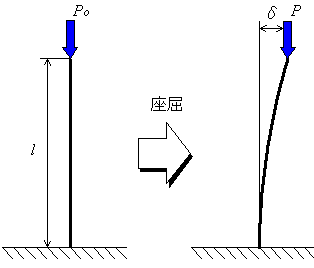
図5.18 座屈

(2)疲れ限度
ここまで延々と話を進めてきてさすがに私も少々疲れてきました.ここでは材料も疲れるんだという話をします.
金属材料は繰り返し応力を受けることにより疲労して破壊することがあります.この場合,比例限度内の応力で破壊にいたりますので注意が必要です.
図5.19に示すように,疲れ破壊が生じる応力と繰り返し数の関係を図示したものをS−N曲線といいます.図より,応力振幅が大きければ少ない繰り返し回数でも壊れ,応力振幅が小さくなると壊れるまでの繰り返し回数は大きくなります.ところが,例えば鋼材では繰り返し数が100万〜1000万回になると,曲線の傾きが変わりほぼ水平になります.これは,これ以下の応力では何回繰り返し応力を受けても疲れないということで,疲れ限度とよばれています.
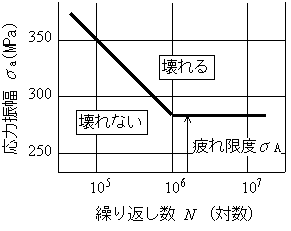
図5.19 S−N曲線
疲れ限度は平均応力(図5.20)の影響を受けるので,図5.21に示すように縦軸に応力振幅をとり,横軸に平均応力をとって疲れ限度を示します.これを疲れ限度線図といい設計で利用されます.
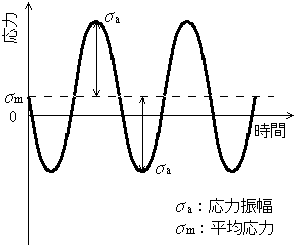
図5.20 応力振幅と平均応力
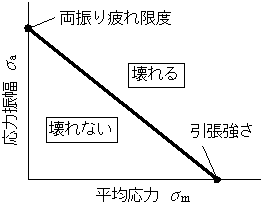
図5.21 疲れ限度線図(Goodman線図)
(3)強度向上のために
さて,金属材料の疲労はどのようにして起こるのでしょうか.定説では,まずどこかに小さなき裂が発生し,それが進展して破壊にいたるといわれています.では,き裂が発生しやすい場所はどこでしょうか.この問題を解く鍵は材料の形状にあります.微小き裂の発生する場所では,図5.22に示すように穴や切欠きなど形状の急変があり,ここに大きな応力が生じています.これを応力集中といいます.
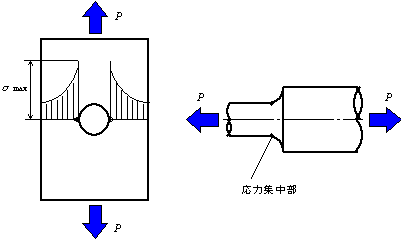
図5.22 応力集中
機械や構造物の破壊は,その大部分が繰り返し応力を受ける部材の応力集中部を起点に,き裂が進展して起こります.このため,設計で応力集中が生じにくい形状とすることがきわめて重要です.
応力集中が発生する部品の形状を変更することで,疲れ強度を向上させることができます.いくつかの対策例をあげます.
(a)コーナーR
応力集中は凹んだ角に生じやすいのです.図5.23に示すように凹んだ角にはコーナーRを付けましょう.
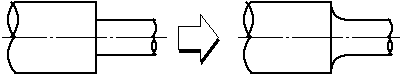
図5.23 コーナーR
(b)応力どめ
図5.24に示すように,もともと材料にき裂がある場合,このまま放置しておいてはすぐに破壊してしまいます.蟻の穴から堤もくずれます.き裂の先端部に応力どめとよばれる円孔を空けて,き裂の進展を防ぎましょう.
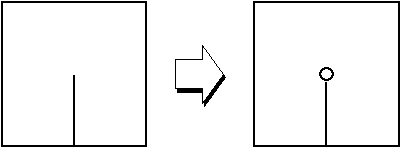
図5.24 応力どめ
(c)近接した切欠き
図5.25に示すように,切欠きなど応力集中が発生する要素が近接して存在するときには応力集中が緩和される場合があります.毒をもって毒を制すですね.
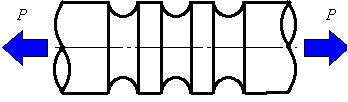
図5.25 近接した複数の切欠き
おしまいに応力集中が生じているかどうかをイメージ的に把握する方法を紹介しましょう.まずは流体力学を勉強することです.材料の応力線を流体の流線と考えてください.流線が密になっている部分に応力が集中しています.もちろん応力線と流線は相似ではありませんが,傾向的には一致します.ここだけの話ですが,機械の強度設計の極意は,流体の流線をイメージしながらコーナーRをつけることかもしれません.
|